Prelab 10

Op-amp circuits are often designed and implemented for signal differentiation and integration. Until recently (before computer-based control), control algorithms (such as PID) containing differentials and integrals were implemented in discrete circuit components. Differentiation is also useful for obtaining velocity measurements from a signal representing a position or determining a signal's frequency (recall the amplitude of the time derivative of a sinusoid is scaled by its frequency). Figure 1 below shows an ideal op-amp integrator and differentiator with input-output relationships that are theoretically correct, but have practical implementation issues discussed below. In this lab, practically realizable differentiators and integrators will be built using op-amps, resistors and capacitors.

1. The Differentiator

• The ideal differentiator is inherently unstable in practice due to the presence of some high frequency noise in every electronic system. An ideal differentiator would amplify this small noise. For instance, if v_noise = Asin(ωt) is differentiated, the output would be v_out = Aωcos(ωt). Even if A = 1μV, when ω = 2π(10MHz), v_out would have an amplitude of 63V! To circumvent this problem, it is traditional to include a series resistor at the input and a parallel capacitor across the feedback resistor as shown in figure 2, converting the differentiator to an integrator at high frequencies for filtering.

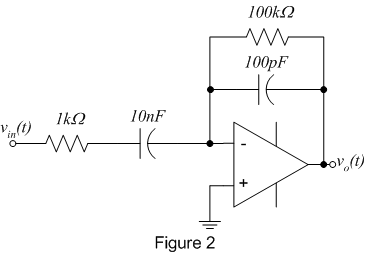
• Wire up the practical op-amp differentiator shown in figure 2 using your op-amp of choice (741 or 356). 
• Drive it (via v_in(t)) with a 1kHz sine wave, a 1kHz square wave, and a 1kHz triangle wave. For each input signal, sketch the input and output waveforms.
• Are the output waveforms and their amplitudes what you would expect, i.e., does the circuit differentiate the input signal?

2. The Integrator

• Op-amps allow you to make nearly perfect integrators such as the practical integrator shown in figure 3.  The circuit incorporates a large resistor in parallel with the feedback capacitor. This is necessary because real op-amps have a small current flowing at their input terminals called the "bias current". This current is typically a few nanoamps, and is neglected in many circuits where the currents of interest are in the microamp to milliamp range. However, if you apply a nanoamp current to a 0.1μF capacitor, it won't take long until it charges and becomes effectively an open circuit not allowing any current to flow! The feedback resistor gives a path for the bias current to flow. The effect of the resistor on the response is negligible at all but the lowest frequencies.

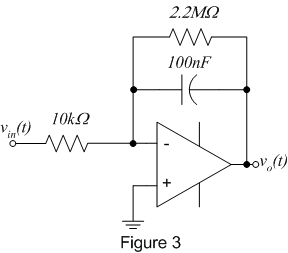
• Wire up the practical op-amp integrator shown in figure 3.
• Drive the input (via v_in(t)) with a 500Hz square wave of 2 V p-p amplitude. Sketch the input and output waveforms.
• Has the input been integrated? 
• Calculate the expected output waveform via integration using the circuit component values and compare to the experimental waveform. 
• Does the amplitude of the output waveform agree with what it should be from the circuit values?
• Repeat using a sine wave and a triangle wave.

© Copyright 2003 New Mexico Institute of Mining and Technology